How To Solve For R
Solving
Functions vs equations
Much of the content of high-school algebra involves "solving." In the typical situation, you have an equation, say \[ 3 x + two = y\] and yous are asked to "solve" the equation for \(10\). This involves rearranging the symbols of the equation in the familiar ways, e.chiliad., moving the \(2\) to the correct hand side and dividing by the \(three\). These steps, originally termed "balancing" and "reduction" are summarized in the original meaning of the arabic word "al-jabr" (that is, 
used by Muhammad ibn Musa al-Khowarizmi (c. 780-850) in his "Compendious Book on Adding by Completion and Balancing". This is where our word "algebra" originates.
Loftier school students are also taught a variety of advertizement hoc techniques for solving in particular situations. For example, the quadratic equation \(a x^2 + b x + c = 0\) tin can be solved by application of the procedures of "factoring," or "completing the square," or use of the quadratic formula: \[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} .\] Parts of this formula tin can be traced back to at least the year 628 in the writings of Brahmagupta, an Indian mathematician, just the consummate formula seems to date from Simon Stevin in Europe in 1594, and was published by René Descartes in 1637.
For some issues, students are taught named operations that involve the changed of functions. For instance, to solve \(\sin(ten) = y\), one only writes down \(x = \arcsin(y)\) without any item on how to find \(\arcsin\) across "use a calculator" or, in the old days, "apply a table from a book."
From Equations to Zeros of Functions
With all of this emphasis on procedures such as factoring and moving symbols back and forth effectually an \(=\) sign, students naturally ask, "How do I solve equations in R?"
The answer is surprisingly simple, but to empathise it, you lot demand to have a different perspective on what it means to "solve" and where the concept of "equation" comes in.
The general form of the problem that is typically used in numerical calculations on the computer is that the equation to be solved is really a function to be inverted. That is, for numerical computation, the problem should be stated similar this:
You have a function \(f(ten)\). Yous happen to know the form of the function \(f\) and the value of the output \(y\) for some unknown input value \(10\). Your problem is to notice the input \(10\) given the function \(f\) and the output value \(y\).
1 way to solve such problems is to notice the inverse of \(f\) . This is often written \(f^{\ -1}\) (which many students understandably simply mistakenly accept to mean \(1/f(x)\)). Just finding the inverse of \(f\) can be very hard and is overkill. Instead, the problem can be handled past finding the zeros of \(f\).
If y'all can plot out the office \(f(10)\) for a range of \(x\), you can hands find the zeros. Just find where the \(x\) where the office crosses the \(y\)-axis. This works for whatsoever office, fifty-fifty ones that are and then complicated that in that location aren't algebraic procedures for finding a solution.
To illustrate, consider the office \(yard()\)
g <- makeFun(sin(x^ ii)* cos(sqrt(ten^ 4 + 3 )-10^ 2) - x + one ~ x) slice_plot(chiliad(x) ~ x, domain(x = -three : 3)) %>% gf_hline(yintercept = 0, color = "red")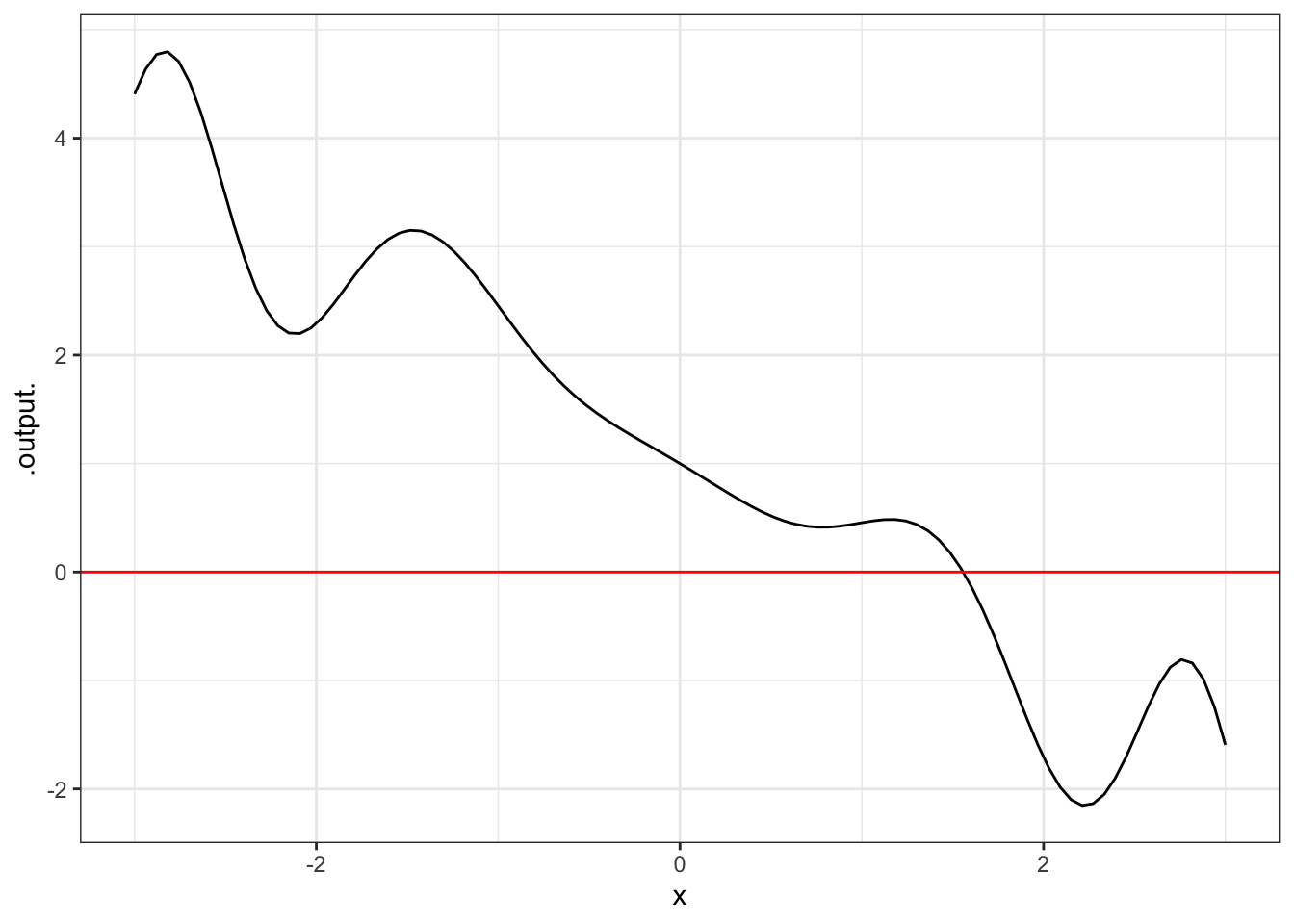 
You can run into easily plenty that the function crosses the \(y\) axis somewhere betwixt \(x=one\) and \(x=2\). You can get more item by zooming in around the guess solution:
slice_plot(g(10) ~ x, domain(10= ane : ii)) %>% gf_hline(yintercept = 0, color = "ruby-red")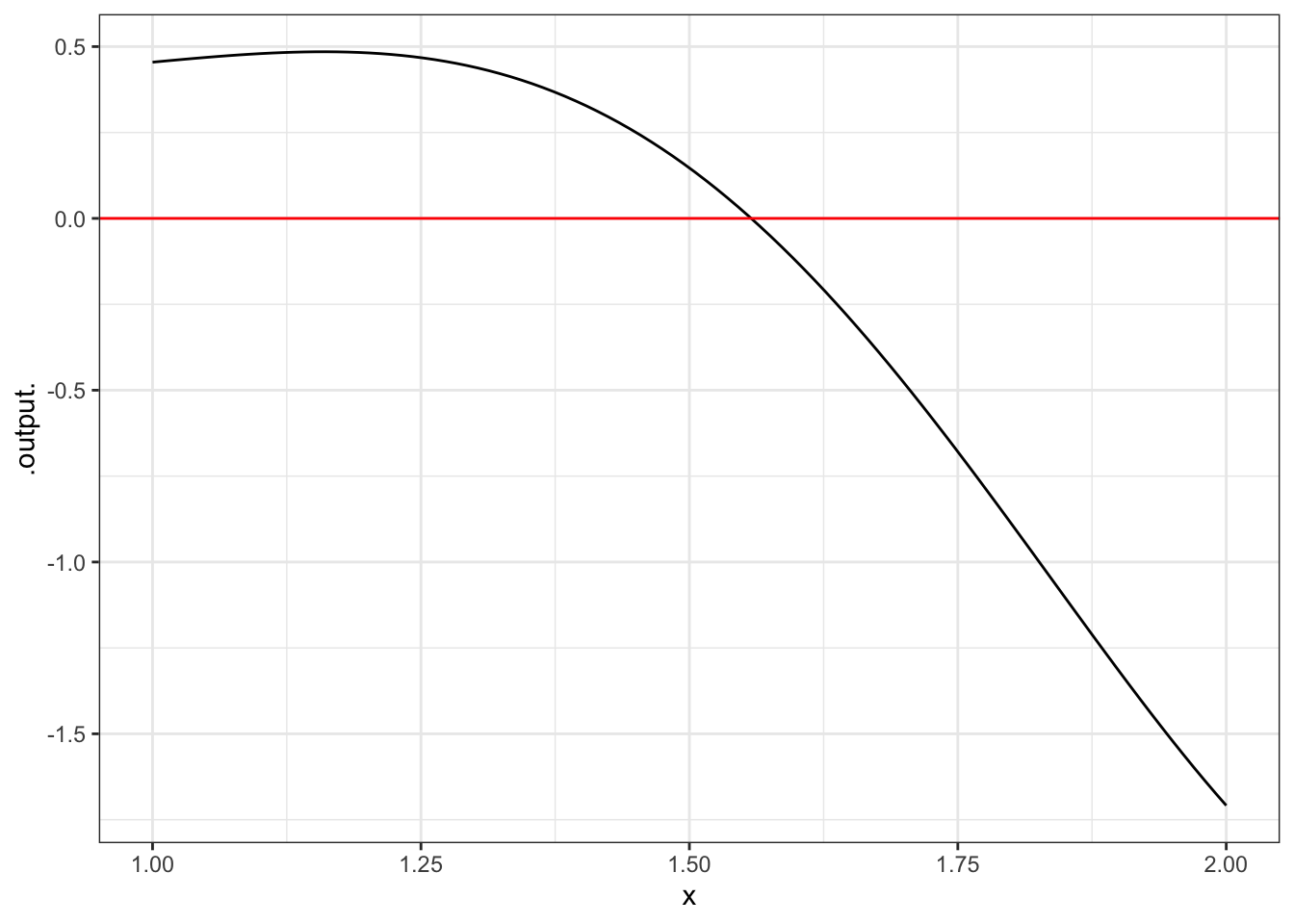 
The crossing is at roughly \(x \approx 1.6\). You could, of form, zoom in further to get a better approximation. Or, you can let the software do this for you:
findZeros(g(x) ~ x, xlim = range(one, 2)) ## x ## 1 1.5576 The argument xlim is used to country where to look for a solution. (Due to a software problems, it's always called xlim fifty-fifty if you lot employ a variable other than x in your expression.)
You lot need only accept a rough idea of where the solution is. For example:
findZeros(g(x) ~ x, xlim = range(- 1000, 1000)) ## x ## i 1.5576 findZeros() will only look within the interval you lot requite information technology. Information technology will do a more precise job if you can state the interval in a narrow way.
Multiple Solutions
The findZeros( ) office volition endeavour to find multiple solutions if they exist. For instance, the equation \(\sin ten = 0.35\) has an infinite number of solutions. Here are some of them:
findZeros( sin(ten) - 0.35 ~ x, xlim= range(- 20,20) ) ## x ## 1 -12.2088 ## ii -9.7823 ## 3 -5.9256 ## four -three.4991 ## v 0.3576 ## six 2.7840 ## seven half-dozen.6407 ## viii 9.0672 ## 9 12.9239 ## ten 15.3504 Note that the equation \(\sin x = 0.35\) was turned into a role sin(3) - 0.35.
Setting up a Problem
Equally the name suggests, findZeros( ) finds the zeros of functions. You can gear up any solution trouble in this course. For example, suppose yous want to solve \(4 + e^{grand t} = 2^{b t}\) for \(b\), letting the parameter \(k\) be \(k=0.00035\). Y'all may, of form, recall how to exercise this problem using logarithms. But here'southward the fix up for findZeros( ):
g <- makeFun(4 + exp(chiliad*t) - 2 ^(b*t) ~ b, k= 0.00035, t= i) findZeros( g(b) ~ b , xlim= range(- 1000, 1000) ) ## b ## 1 ii.322 Notation that numerical values for both \(b\) and \(t\) were given. But in the original trouble, at that place was no statement of the value of \(t\). This shows one of the advantages of the algebraic techniques. If you solve the problem algebraically, y'all'll quickly meet that the \(t\) cancels out on both sides of the equation. The numerical findZeros( ) function doesn't know the rules of algebra, so information technology can't effigy this out. Of course, you can try other values of \(t\) to make sure that \(t\) doesn't matter.
findZeros( chiliad(b, t= ii) ~ b, xlim= range(- 1000,yard) ) ## b ## 1 1.1611 Exercises
Practise 1
Solve the equation \(\sin(\cos(x^2) - x) - x = 0.v\) for \(10\). {0.0000,0.1328,0.2098,0.3654,0.4217}
Respond:
findZeros( sin(cos(x^ two) - ten) -x - 0.5 ~ x, xlim= range(- x,10)) ## x ## i 0.2098 Exercise ii
Find any zeros of the function \(three e^{- t/5} \sin(\frac{2\pi}{two} t)\) that are between \(t=1\) and \(t=10\).
- There aren't whatsoever zeros in that interval.}
- There aren't any zeros at all!}
- $ 2, four, 6, eight$}
- $ one, three, 5, 7, ix$}
- { \(one, 2, 3, 4, 5, vi, seven, 8, 9\) }
ANSWER:
findZeros( iii * exp(-t/ 5)* sin(pi*t) ~ t, xlim= range(1,x)) ## t ## 1 0 ## 2 1 ## 3 2 ## 4 3 ## 5 4 ## 6 v ## 7 6 ## 8 7 ## 9 viii ## 10 9 Exercise 3
Use findZeros() to find the zeros of each of these polynomials:
- \(three x^two +7 x - ten\)
Where are the zeros? a. \(10=-3.33\) or \(1\) b. \(10=3.33\) or \(1\) c.\(10=-iii.33\) or \(-ane\) d.\(ten=3.33\) or \(-one\) due east. No zeros
ANSWER:
findZeros( 3 *10^ ii + vii *ten - 10 ~ ten, xlim= range(- 100,100)) ## ten ## 1 -3.3334 ## 2 i.0000 - \(4 x^two -2 ten + twenty\)
Where are the zeros? a. \(ten=-3.33\) or \(1\) } b. \(x=3.33\) or \(1\)} c.\(x=-3.33\) or \(-1\)} d.\(ten=3.33\) or \(-ane\)} eastward. No zeros
- \(2 10^iii - 4x^2 - 3x - 10\)
Which one of these is a zero? {-1.0627,0,1.5432,one.8011,two.1223,3.0363,none}
Answer:
findZeros(2 *ten^ 3 - 4 *ten^ 2 - 3 *10 - x ~ 10, xlim= c(- 10,10)) ## x ## 1 3.0363 - \(7x^4 - 2 x^3 - 4x^ii - 3x - 10\)
Which one of these is a aught? {-1.0627,0,i.5432,1.8011,2.1223,3.0363,none}
Answer:
findZeros( 7 *x^ four -2 *x^ three - 4 *x^ 2 - 3 *ten - 10 ~ x, xlim= c(- 10,x)) ## x ## ane -ane.0628 ## ii one.4123 - \(6 x^5 -7x^4 - ii x^3 - 4x^2 - 3x - 10\)
Which 1 of these is a zero? {-1.0627,0,1.5432,ane.8012,2.1223,3.0363,none}
Respond:
findZeros( half dozen *x^ 5-seven *x^ 4 -two *ten^ 3 - 4 *x^ 2 - 3 *x - ten ~ x, xlim= c(- 10,ten)) ## x ## 1 1.8012 
How To Solve For R,
Source: https://dtkaplan.github.io/RforCalculus/solving.html
Posted by: phillipsalthatede.blogspot.com
0 Response to "How To Solve For R"
Post a Comment